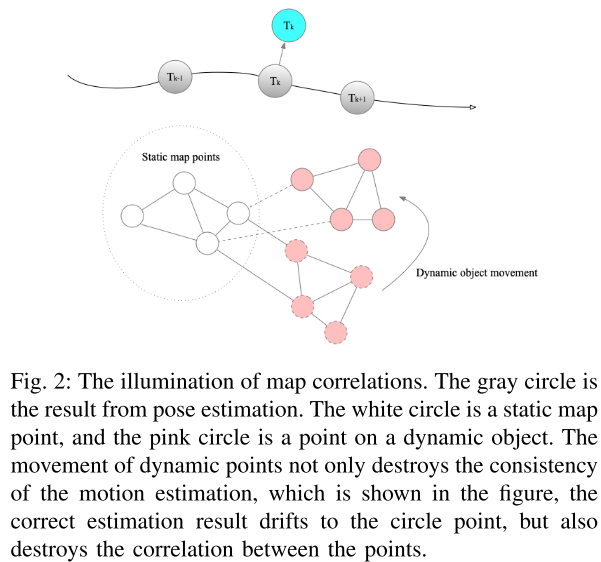
If the realative position between two points remains consistent over time, there is a correlation between them, and they are considered to be moving together rigidly. If not, they are considered to have to correlation and to be in separate groups.
A sparse graph is created from all map pints using Delaunay triangulation.
It should be noted that the movement of dynamic objects also breaks the correlations between the static and dynamic groups of map points. Therefore, we believe that the geometry prior of correlations is the key to solve the dynamic problem.
The measurement of correlations between point pi and pj at time k could be the form:
$z_{ijk} = h(l_{ijk})+n_{ijk}$
where $l_{ijk} = p_{ik} - p_{jk}$. h() is the correlation measurement model for the sensor and nijk also is the additive Gaussian noise. Therefore, for each observation of correlations between points, the error term is:
$e_{z,ijk}(x_p)=z_{ijk} - h(l_{ijk})$
where $x_p$ is the **subset** of all states x including all map points:
$x = \{ T_1, ..., T_k, p_1, ..., p_M\}$
- $T_k$ is the transfromation matrix representing the pose of rotbot at time k
- $p_i$ represents the position of i-th map points
Therefore, the following objective function could be defined:
$J_p(x_p) = \frac{1}{2} \sum_{ijk} {e_{z,ijk}(l_{ijk})^T R_{ik}^{-1} e_{z,ijk(l_{ijk})}}$
Outliers, which are considered as the disconnected edges, could be removed while minimizing the cost function using RANSAC.
The disconnected results of the point cloud are divided into different groups. In most scenarios, we know that the static maps grow incrementally, so the size of static maps can be considered as much larger than dynamic part. At the same time, once the static map group is determined, the group that do not belong to the static group in the subsequent frames can be directly removed. Therefore, based on above results, the static group and connections always are maintained。
地图点会分成两部分：动态部分与静态部分（静态组与动态组）。静态部分会稳定的持续增长，将不在静态组的点视为动态点。
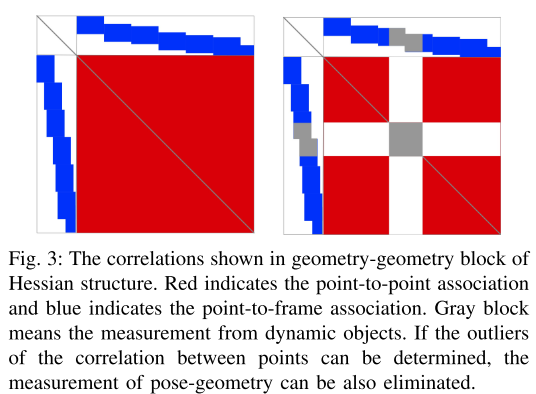
In addition to the outliers that are removed in pose-geometry block, the optimization with RANSAC could remove non-consistency correlations in geometry-geometry blocks. **However, the introduction of correlations between geometry parameters render the joint optimization infeasible in real time**. Therefore, the optimization of connected points is running separately in the implementation.
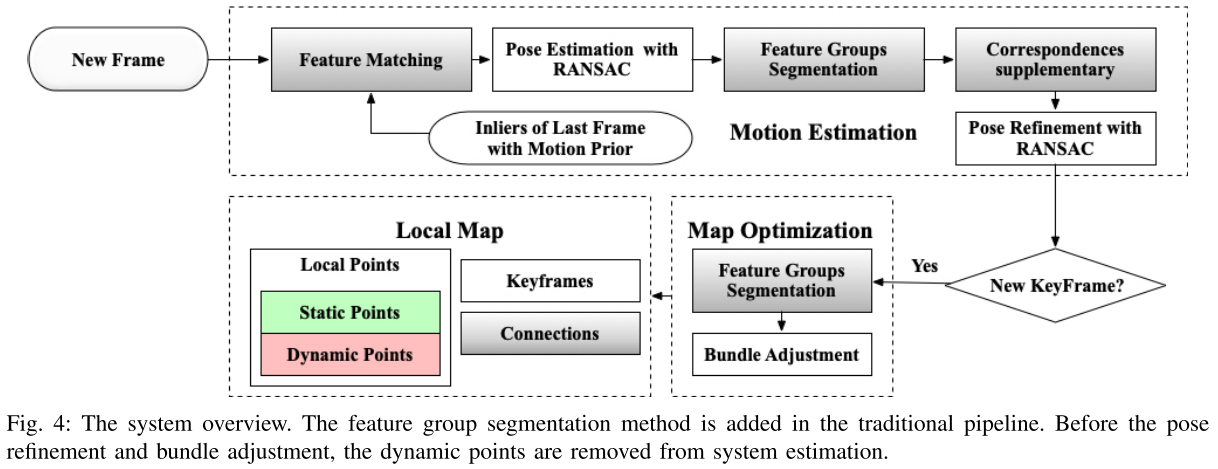
### SLAM in Dynamic Environments
- Input：color and detph images from an RGB-D camera
- Build on the ORB-SLAM2
Feature Groups Segmentation:
If the geometry-geometry block is not diagonal, some efficient methods proposed for sparse matrix cannot be applied directly. Thus, how to construct correlations, divide the matched feature points into different groups and separate the moving objects from the background is the key of the proposed method.
本文使用了Delaunay三角剖分算法。
Delaunay三角剖分有最大化最小角，“最接近于规则化的“的三角网和唯一性（任意四点不能共圆）两个特点。
(Referred from [https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
【定义】三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：
1.除了端点，平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。
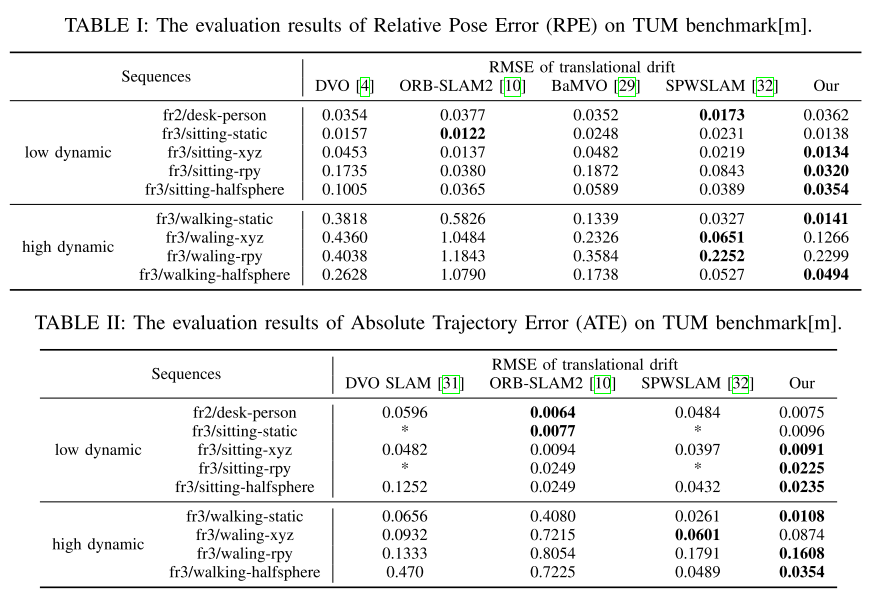
### Experiment
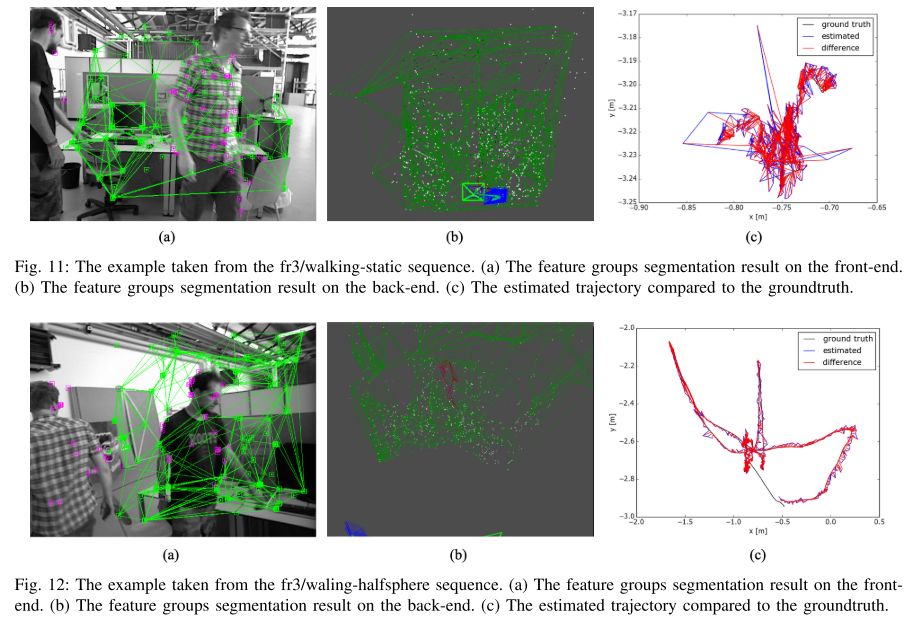
### References
- Dai, W., Zhang, Y., Li, P., & Fang, Z. (2018). RGB-D SLAM in Dynamic Environments Using Points Correlations. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://arxiv.org/pdf/1811.03217v1.pdf
- Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. (1996). The Quickhull Algorithm for Convex Hulls. *ACM Transactions on Mathematical Software*, *22*(4), 469–483. https://doi.org/10.1145/235815.235821
- [人脸变形基础-Delaunay Triangulation](https://www.jianshu.com/p/7b7844d7976d)
- [Delaunay三角剖分算法]([https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
DSLAM: RGB-D SLAM in Dynamic Environments Using Points Correlations [论文学习]
# 2018-RGB-D SLAM in Dynamic Environments Using Points Correlations
又称为DSLAM.
The main contributions of this paper are:
- The integration of geometry prior is proposed to find the points group with consistency.
- A novel feature groups segmentation method is proposed to resist the disturbance caused by dynamic objects. It separates dynamic points group from the part of the local map.
- The proposed method is evaluated and compared to advanced methods on a public RGB-D benchmark. The results demonstrate the accuracy and efficiency of the system in dynamic environments.
If the realative position between two points remains consistent over time, there is a correlation between them, and they are considered to be moving together rigidly. If not, they are considered to have to correlation and to be in separate groups.
A sparse graph is created from all map pints using Delaunay triangulation.
It should be noted that the movement of dynamic objects also breaks the correlations between the static and dynamic groups of map points. Therefore, we believe that the geometry prior of correlations is the key to solve the dynamic problem.
The measurement of correlations between point pi and pj at time k could be the form:
$z_{ijk} = h(l_{ijk})+n_{ijk}$
where $l_{ijk} = p_{ik} - p_{jk}$. h() is the correlation measurement model for the sensor and nijk also is the additive Gaussian noise. Therefore, for each observation of correlations between points, the error term is:
$e_{z,ijk}(x_p)=z_{ijk} - h(l_{ijk})$
where $x_p$ is the **subset** of all states x including all map points:
$x = \{ T_1, ..., T_k, p_1, ..., p_M\}$
- $T_k$ is the transfromation matrix representing the pose of rotbot at time k
- $p_i$ represents the position of i-th map points
Therefore, the following objective function could be defined:
$J_p(x_p) = \frac{1}{2} \sum_{ijk} {e_{z,ijk}(l_{ijk})^T R_{ik}^{-1} e_{z,ijk(l_{ijk})}}$
Outliers, which are considered as the disconnected edges, could be removed while minimizing the cost function using RANSAC.
The disconnected results of the point cloud are divided into different groups. In most scenarios, we know that the static maps grow incrementally, so the size of static maps can be considered as much larger than dynamic part. At the same time, once the static map group is determined, the group that do not belong to the static group in the subsequent frames can be directly removed. Therefore, based on above results, the static group and connections always are maintained。
地图点会分成两部分：动态部分与静态部分（静态组与动态组）。静态部分会稳定的持续增长，将不在静态组的点视为动态点。
In addition to the outliers that are removed in pose-geometry block, the optimization with RANSAC could remove non-consistency correlations in geometry-geometry blocks. **However, the introduction of correlations between geometry parameters render the joint optimization infeasible in real time**. Therefore, the optimization of connected points is running separately in the implementation.
### SLAM in Dynamic Environments
- Input：color and detph images from an RGB-D camera
- Build on the ORB-SLAM2
Feature Groups Segmentation:
If the geometry-geometry block is not diagonal, some efficient methods proposed for sparse matrix cannot be applied directly. Thus, how to construct correlations, divide the matched feature points into different groups and separate the moving objects from the background is the key of the proposed method.
本文使用了Delaunay三角剖分算法。
Delaunay三角剖分有最大化最小角，“最接近于规则化的“的三角网和唯一性（任意四点不能共圆）两个特点。
(Referred from [https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
【定义】三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：
1.除了端点，平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。
### Experiment
### References
- Dai, W., Zhang, Y., Li, P., & Fang, Z. (2018). RGB-D SLAM in Dynamic Environments Using Points Correlations. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://arxiv.org/pdf/1811.03217v1.pdf
- Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. (1996). The Quickhull Algorithm for Convex Hulls. *ACM Transactions on Mathematical Software*, *22*(4), 469–483. https://doi.org/10.1145/235815.235821
- [人脸变形基础-Delaunay Triangulation](https://www.jianshu.com/p/7b7844d7976d)
- [Delaunay三角剖分算法]([https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
If the realative position between two points remains consistent over time, there is a correlation between them, and they are considered to be moving together rigidly. If not, they are considered to have to correlation and to be in separate groups.
A sparse graph is created from all map pints using Delaunay triangulation.
It should be noted that the movement of dynamic objects also breaks the correlations between the static and dynamic groups of map points. Therefore, we believe that the geometry prior of correlations is the key to solve the dynamic problem.
The measurement of correlations between point pi and pj at time k could be the form:
$z_{ijk} = h(l_{ijk})+n_{ijk}$
where $l_{ijk} = p_{ik} - p_{jk}$. h() is the correlation measurement model for the sensor and nijk also is the additive Gaussian noise. Therefore, for each observation of correlations between points, the error term is:
$e_{z,ijk}(x_p)=z_{ijk} - h(l_{ijk})$
where $x_p$ is the **subset** of all states x including all map points:
$x = \{ T_1, ..., T_k, p_1, ..., p_M\}$
- $T_k$ is the transfromation matrix representing the pose of rotbot at time k
- $p_i$ represents the position of i-th map points
Therefore, the following objective function could be defined:
$J_p(x_p) = \frac{1}{2} \sum_{ijk} {e_{z,ijk}(l_{ijk})^T R_{ik}^{-1} e_{z,ijk(l_{ijk})}}$
Outliers, which are considered as the disconnected edges, could be removed while minimizing the cost function using RANSAC.
The disconnected results of the point cloud are divided into different groups. In most scenarios, we know that the static maps grow incrementally, so the size of static maps can be considered as much larger than dynamic part. At the same time, once the static map group is determined, the group that do not belong to the static group in the subsequent frames can be directly removed. Therefore, based on above results, the static group and connections always are maintained。
地图点会分成两部分：动态部分与静态部分（静态组与动态组）。静态部分会稳定的持续增长，将不在静态组的点视为动态点。
In addition to the outliers that are removed in pose-geometry block, the optimization with RANSAC could remove non-consistency correlations in geometry-geometry blocks. **However, the introduction of correlations between geometry parameters render the joint optimization infeasible in real time**. Therefore, the optimization of connected points is running separately in the implementation.
### SLAM in Dynamic Environments
- Input：color and detph images from an RGB-D camera
- Build on the ORB-SLAM2
Feature Groups Segmentation:
If the geometry-geometry block is not diagonal, some efficient methods proposed for sparse matrix cannot be applied directly. Thus, how to construct correlations, divide the matched feature points into different groups and separate the moving objects from the background is the key of the proposed method.
本文使用了Delaunay三角剖分算法。
Delaunay三角剖分有最大化最小角，“最接近于规则化的“的三角网和唯一性（任意四点不能共圆）两个特点。
(Referred from [https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
【定义】三角剖分：假设V是二维实数域上的有限点集，边e是由点集中的点作为端点构成的封闭线段, E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G，该平面图满足条件：
1.除了端点，平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面，且所有三角面的合集是散点集V的凸包。
### Experiment
### References
- Dai, W., Zhang, Y., Li, P., & Fang, Z. (2018). RGB-D SLAM in Dynamic Environments Using Points Correlations. IEEE Robotics and Automation Letters, 2(4), 2263–2270. https://arxiv.org/pdf/1811.03217v1.pdf
- Barber, C. B., Dobkin, D. P., & Huhdanpaa, H. (1996). The Quickhull Algorithm for Convex Hulls. *ACM Transactions on Mathematical Software*, *22*(4), 469–483. https://doi.org/10.1145/235815.235821
- [人脸变形基础-Delaunay Triangulation](https://www.jianshu.com/p/7b7844d7976d)
- [Delaunay三角剖分算法]([https://baike.baidu.com/item/Delaunay%E4%B8%89%E8%A7%92%E5%89%96%E5%88%86%E7%AE%97%E6%B3%95/3779918?fr=aladdin](https://baike.baidu.com/item/Delaunay三角剖分算法/3779918?fr=aladdin))
No comments